Dicen los que saben que la teoría de grafos vió su origen en el siglo XVIII de la mano del famosísimo matemático suizo, Leonhard Euler. La historia cuenta que todo surgió al tratar de resolver el problema de los puentes de Köningsberg (ciudad rusa conocida en español como Kaliningrado) en donde había cuatro islas conectadas por siete puentes (como se muestra en la Figura 1A). La idea era buscar la forma de cruzar los siete puentes una sola vez en un solo recorrido.
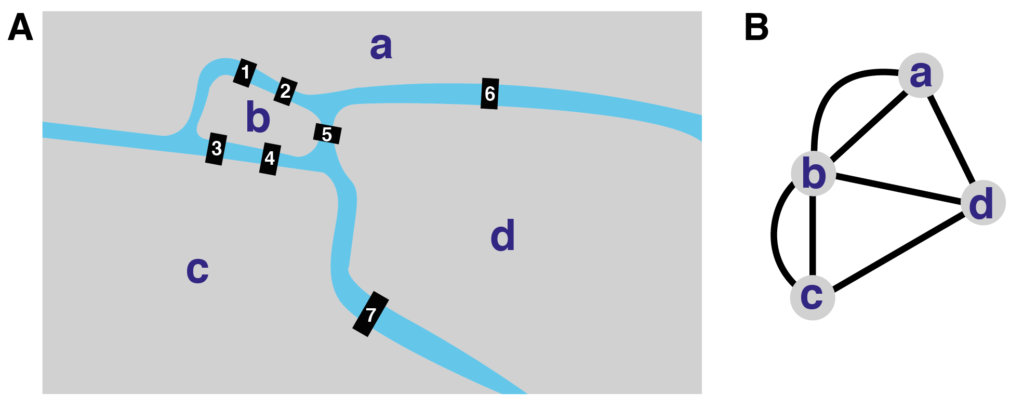
Para resolver el problema, Euler dibujó la ciudad representando las cuatro islas como nodos de una red, y los siete puentes como enlaces entre los nodos (Figura 1B).
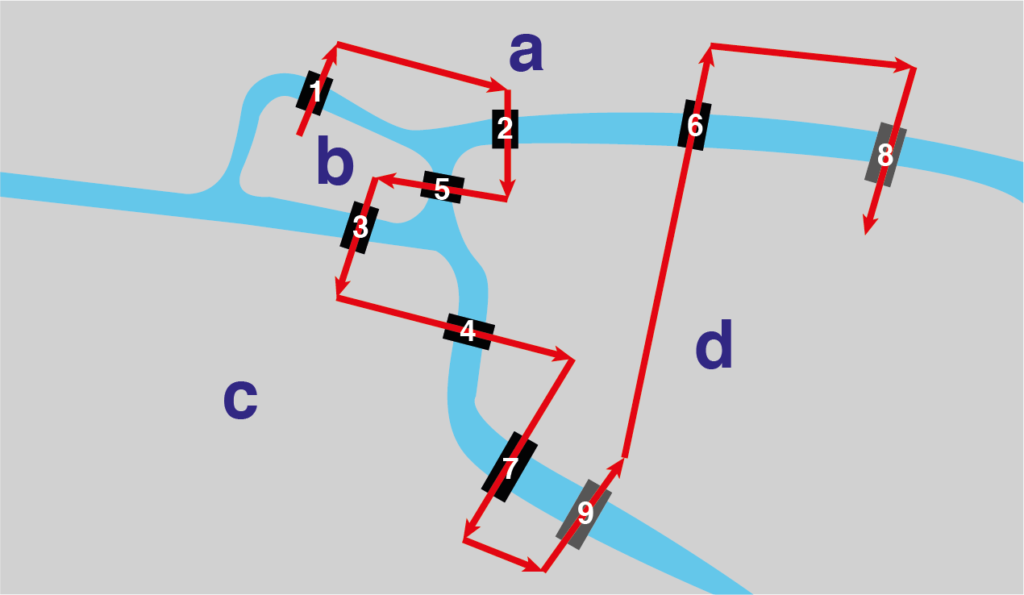
Después de romperse la cabeza un buen rato (supongo), Euler llegó a la conclusión de que la solución que buscaba no existía. Sin embargo, la construcción de dos puentes más, para un total de 9, permitió una posible solución (Figura 2), a lo que se le conoce como el camino de Euler o camino Euleriano. Pero el chiste de todo esto es que en el proceso se empezó a pensar en términos de nodos, enlaces, grado (en este ejemplo, el grado de una isla o nodo sería el número de puentes entre esa y otras islas o nodos). Esto sentó las bases de la teoría de grafos como la conocemos en nuestros tiempos.
Aunque la teoría de grafos se ha visto desde sus origen como una disciplina puramente matemática, sus aplicaciones en diversas disciplinas, llevó inevitablemente a su aplicación para el análisis de sistemas biológicos completos, como es el caso de los islotes pancreáticos.
Los islotes pancreáticos, mostrados esquemáticamente en la Figura 3, son pequeños grupos de células localizados en el páncreas. Se componen de diferentes tipos de células, entre las que destacan las células ɑ, β y δ, secretoras de glucagón, insulina y somatostatina, respectivamente, hormonas fuertemente involucradas en la regulación de la glucosa en sangre, también conocida popularmente como azúcar en la sangre, y como consecuencia, al desarrollo de enfermedades graves como la diabetes en sus diferentes formas. Al ser los islotes pancreáticos un conjunto de células que se comunican entre ellas (como las islas de Kaliningrado vía los puentes), las células, en una interpretación utilizando la teoría de grafos, pueden verse como los nodos y las diferentes formas de comunicación entre ellas, como los enlaces.
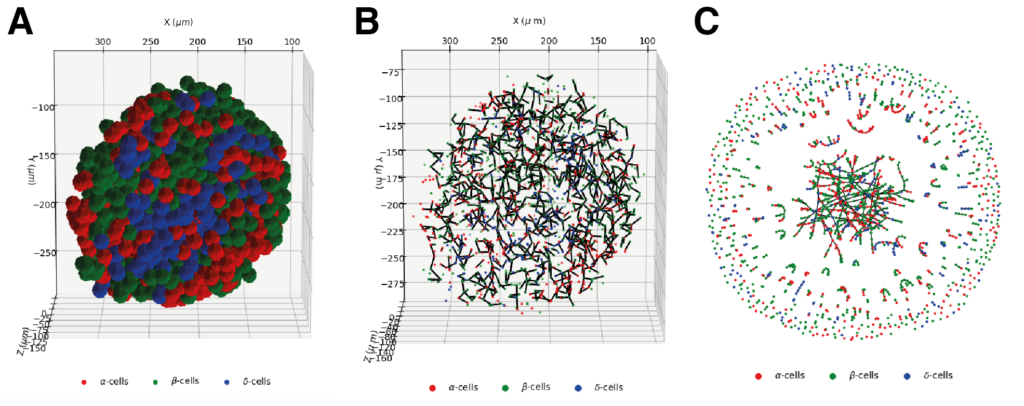
Los avances de la teoría de grafos como un campo multidisciplinario es la base de la ahora conocida como teoría o ciencia de redes, ampliamente utilizada en campos tan variados como la biología, el análisis del tráfico vehicular, redes computacionales, y un largo etcétera. En el caso de los islotes pancreáticos, la teoría o ciencia de redes ha sido utilizada para analizar las conexiones funcionales y estructurales entre las células que los componen, surgiendo como una herramienta que nos permitirá enlazar su organización, composición y distribución con la conectividad y los aspectos funcionales, aspecto clave para poder alcanzar un mayor entendimiento de las alteraciones sufridas por los islotes como consecuencia de enfermedades como la diabetes tipo 2.
